Understanding Linear Regression – The Ordinary Least Squares

Linear Regression is considered as one of the most basic and widely used Machine Learning techniques. Statistical techniques of linear regression are used to conduct the predictive analysis to predict numeric and real variables. Occasionally you will find yourself reading about “linear regression and Ordinary Least Squares” in connection with a book or research article. If we were to use the words “least squares” and “regression,” you might now that these phrases are referring to linear regression, but how do they relate to each other?

Introduction: What is Linear Regression

Linear regression is a statistical technique that is used to model the relationships between dependent variables and one or more independent variables.The linear relationship, which is built by linear regression, gives a brief explanation of the relation between the value of the dependent variable and the values of the independent variable. The value of the dependent variable changes when the value of the independent variable is changed due to the linear relationship between these variables. The mathematical representation of linear regression can be represented as: Alpha, Beta = Alpha is the point where the line is the intercept, Beta is the coefficient of Input Variable Epsilon = That symbol represents the error rate Y = It represents the target variable which is also called the dependent variable. X = It represents the predictor variable which is also called an independent variable. There are many different ways to compute linear regression, but the most common methods to compute relationship coefficients are

• Ordinary Least Squares (OLS)
• Gradient Descent

We will discuss Gradient Descent in upcoming articles, for now, let’s have a look at OLS method.

The Ordinary Least Squares Method

The OLS method is a statistical technique that is used to estimate the parameters of a linear regression model. The method is based on the principle of least squares, which states that the best estimate of the parameters is obtained by minimizing the sum of squared residuals. In other words, OLS finds the line of best fit by minimizing the distance between the data points and the line itself. Linear Regression is utilized to build a connection among a dependent variable and one or many independent variables. Smallest Square Error is referred to by the term “least squares”. The other method, such as Generalized and Maximum likelihood, are considered other techniques of OLS.

Mathematics of OLS

For a dataset with k examples, the OLS method approaches to find optimal coefficients to satisfy the follow equation.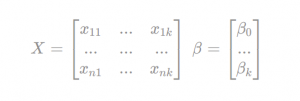 Similarly for these multiple independent variables, we can construct matrix of these input variables. To find the values that minimize the error, we can rewrite the equation as 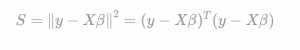Now upon re-arranging the first equation, we can write the following equation to calculate target beta-vector. We can see two major products here. First, the product of input matrix with the transpose of this input matrix. Second, the product transpose of input matrix with the dependent variable. Finally the product of these two sub products will result in beta-vector calculation.

Assumptions of OLS Method

One of the assumptions of OLS is that there is a linear relationship between the dependent variable and the explanatory variables. This means that as the values of the explanatory variables change, so too will the values of the dependent variable. Another assumption of OLS is that there is no multicollinearity among the explanatory variables. Multicollinearity occurs when two or more of the explanatory variables are highly correlated with each other. This can lead to problems with interpretability because it can be difficult to determine which variable is having the biggest impact on the dependent variable.